FOURIER-TRANSFORMATION
The Fourier Transform , in essence, decomposes or separates a waveform
or function into sinusoids of different frequency which sum to the original
waveform. It identifies or distinguishes the different frequency sinusoids and
their respective amplitudes.
The Fourier Transform as a mathematical concept
The Fourier Transform is based on the discovery that it is possible to take
any periodic fuction of time x(t) and resolve it into an equivalent infinite
summation of sine waves and cosine waves with frequencies that start at 0 and
increase in integer multiples of a base frequency f0 = 1/T, where T is the pe-
-riod of x(t).
Historical Perspective::
Joseph Fourier (1768-1830) was a french mathematician and physicist who,
because of his interest in heat conduction, developed a mathematical method for
the representation of any discontinuous function in space or time in terms of a
much simpler trigonometric series of continuous cosine or sine functions. Such
a series is referred to as a Fourier Series and the process of dissection into
cosine and/or sine components is called Fourier Analysis . The opposite or
inverse operation, recombining cosine and/or sine functions, is called Fourier
synthesis.
If a metal bar is heated, the temprature of the bar is highest at the point
where it is heated and this heat then spreads through the whole bar. Taking
temperature as a function of distance along the bar we see that this is an
example of a discontinuous function. Fourier realised that, if the temperature
was decomposed into continuous sinusoidal curves having 1,2,3 or more cycles
along the bar, then summation of these would yield a good approximation of the
original discontinuous function. The more curves added to Fourier series, the
better the agreement of the Fourier synthesis with the experimental measurement.
Any wave function can be defined in terms of amplitude, A , and wave-length,
 , or frequency, v . A full description of such a wave also requires defini-
-tion of a phase, phi . A simple one-dimensional wave-function, f(x), specif-
-ies the height of the wave at any horizontal point x where x is defined in
terms of wavelength such that x=1=
, or frequency, v . A full description of such a wave also requires defini-
-tion of a phase, phi . A simple one-dimensional wave-function, f(x), specif-
-ies the height of the wave at any horizontal point x where x is defined in
terms of wavelength such that x=1= . This wave function could be represented
as either a sine or a cosine function as follows:
. This wave function could be represented
as either a sine or a cosine function as follows:
 or
or
 The term 2pi appears because there are 2 radians per wavelength. Fourier
analysis of complex wave functions dissociates them into a Fourier series of
simple wave functions such as f(x). We could write a Fourier series containing
n terms as
The term 2pi appears because there are 2 radians per wavelength. Fourier
analysis of complex wave functions dissociates them into a Fourier series of
simple wave functions such as f(x). We could write a Fourier series containing
n terms as

 This shows that any complex wave can be expressed as a composite of simpler
cosine or sine waves.
If a complex discontinuous function is periodic (although this is not essen-
-tial ) with a period T such that f ( t + T ) = f ( t ), it may be represented
as a Fourier series of the form
This shows that any complex wave can be expressed as a composite of simpler
cosine or sine waves.
If a complex discontinuous function is periodic (although this is not essen-
-tial ) with a period T such that f ( t + T ) = f ( t ), it may be represented
as a Fourier series of the form
 where t is time, n is the number of components in the series, i is the imagi-
-nary number (= -1)1/2 and a, b, c etc. are coefficients describing the indi-
-vidual waves in the series.
This mathematically expresses the fact that a discontinuous function can be
dissected into individual sine/cosine wave functions which may in turn be
summed to arrive at an expression for it as a function ( in this case ) of time.
The relationship between the two sets of functions can be generalised with a
pair of equations which are Fourier transforms of each other.
where t is time, n is the number of components in the series, i is the imagi-
-nary number (= -1)1/2 and a, b, c etc. are coefficients describing the indi-
-vidual waves in the series.
This mathematically expresses the fact that a discontinuous function can be
dissected into individual sine/cosine wave functions which may in turn be
summed to arrive at an expression for it as a function ( in this case ) of time.
The relationship between the two sets of functions can be generalised with a
pair of equations which are Fourier transforms of each other.
 where i2 = -1.
A good practical analogy for Fourier analysis is the diffraction of white light
from the sun after passage through a prism into waves of individual frequency
and amplitude. The strength of sunlight incident on the prism may be expected to
vary with time which, in turn leads to variation in the amplitude of each
diffracted frequency. The prism therefore acts to transform a strength-time
domain into an amplitude-frequency domain.
The Fourier transform is special because the equation relating sets of numbers
which can be interconverted by the Fourier transform contains sine and cosine
terms allowing us to relate the complex wave to a series of simpler waves in a
fixed and meaningful way. This allows us to determine unknown discontinuous
experimental functions such as the electron density of an atom ( a function in
space ) or the electromagnetic spectrum of a molecule ( the time-inverse
function, frequency ).
The reason the Fourier transform is so widely used is that it offers specific
computational advantages over other mathematical approaches. However
complex the Fourier series, it is related to the original function by a
comparatively simple equation making it possible to move from the real-world
domain of space or time to the Fourier domain of frequency, phase and
amplitude. Moreover, considerable error can accumulate due to shortcomings in
real-world experimental systems such as those used in diffraction or spectroscopy.
Development of fast Fourier transform algorithm has facilitated very rapid
calculation by computer in the Fourier domain which can smooth out and
diminish this error resulting in a more accurate overall measurement. The
Fourier transform therefore provides a computationally versatile tool to analyse
complex functions arising from experimental measurements by dissecting them
into simpler wave functions which can be used to determine experimental
unknowns.
FFT-FAST FOURIER TRANSFORMATION IN BIOLOGICAL SEQUENCE ANALYSIS
where i2 = -1.
A good practical analogy for Fourier analysis is the diffraction of white light
from the sun after passage through a prism into waves of individual frequency
and amplitude. The strength of sunlight incident on the prism may be expected to
vary with time which, in turn leads to variation in the amplitude of each
diffracted frequency. The prism therefore acts to transform a strength-time
domain into an amplitude-frequency domain.
The Fourier transform is special because the equation relating sets of numbers
which can be interconverted by the Fourier transform contains sine and cosine
terms allowing us to relate the complex wave to a series of simpler waves in a
fixed and meaningful way. This allows us to determine unknown discontinuous
experimental functions such as the electron density of an atom ( a function in
space ) or the electromagnetic spectrum of a molecule ( the time-inverse
function, frequency ).
The reason the Fourier transform is so widely used is that it offers specific
computational advantages over other mathematical approaches. However
complex the Fourier series, it is related to the original function by a
comparatively simple equation making it possible to move from the real-world
domain of space or time to the Fourier domain of frequency, phase and
amplitude. Moreover, considerable error can accumulate due to shortcomings in
real-world experimental systems such as those used in diffraction or spectroscopy.
Development of fast Fourier transform algorithm has facilitated very rapid
calculation by computer in the Fourier domain which can smooth out and
diminish this error resulting in a more accurate overall measurement. The
Fourier transform therefore provides a computationally versatile tool to analyse
complex functions arising from experimental measurements by dissecting them
into simpler wave functions which can be used to determine experimental
unknowns.
FFT-FAST FOURIER TRANSFORMATION IN BIOLOGICAL SEQUENCE ANALYSIS
The analysis of correlations in DNA sequences is an important complement to
experimental studies to identify protein coding genes in genomic DNA. Several
groups have tried Fourier transformation as a means to identify the protein
coding genes (Ramaswamy et al., 1999; Herzel et al., 1999; Yan et al., 1998;
Tiwari et al., 1997; Widom, 1996). What is the basis to use FT on biopolymers?
The answer lies in the composition of the DNA sequence itself.
Tandem repeats and periodic clusters are often found in biological sequences
(DNA and Proteins) and locating and characterizing them may provide certain
information about the structural and functional characteristics of the mole-
-cule. In the recent past two methods have emerged to locate exact or approx-
-imate repeat regions, Fourier analysis and internal homology study.
The search for periodicity in the gene sequences has in the past has produced
some interesting ideas on the origin of the genetic code and the principles
underlying its construction. Analyzing the coding sequences for RNY periodicity
Shepherd, (1982) observed that codons of RNY (purine=R; any=N; pyrimidine=Y)
form seem to be the predominant codon structure in most DNA sequences, sugge-
-sting it to be the most primitive codon. A primitive message composed exclu-
-sively of RNY codons could have been translated in only one of 3 possible
frames, circumventing the need for special start signals to fix the reading
frame. Interestingly, among the 8 amino acids specified by RNY in today's code
(GLY, ILE, THR, ASN, SER, VAL, ALA & ASP) are amino acids that are most likely
to have been generated by prebiotic synthesis, as well as those that often
appear in meteorites (Watson et al., 1987).
Tsonis et al., (1991) employed Fourier analysis of DNA coding and non-coding
sequences in an attempt to identify possible patterns in gene sequences. They
found that while intronic sequences show a rather random pattern, coding seq-
-uences show periodicities and in particular a periodicity of 3. They inferred
that the predominant presence of codons all starting from the same base could
confer the observed periodicities.
Modern genetic information carrying DNA sequences are thought to have evolved
from ancestral primordial blocks which were single-stranded (RNA) oligonucle-
-otides produced by random polymerization of nucleotides. Discovery of RNA
introns, that can act as enzyme, points to the fact that these blocks could be
replicated or fused to produce repeating units without use of proteins. Some
authors have suggested that these short repeating units formed the basis for
the generation of longer sequences by becoming progressively longer and less
homologous to each other.
ELABORATION OF THE PERIODICITY FOUND IN THE SPECTRA::
In order to completely understand the properties of the sequences that are
imprinted on the Fourier spectra let us consider the periodic sequence
A--A--A--A--..... where blanks can be filled randomly by A, C, G or T. This
sequence shows a periodicity of three because of the repetition of the base A.
The spectral density of such sequence is significantly non-zero only at one
frequency (0.33) which corresponds to the perfect periodicity of base A
(1/0.333=3.0). In other words, for this sequence a continuous background does
not exist.
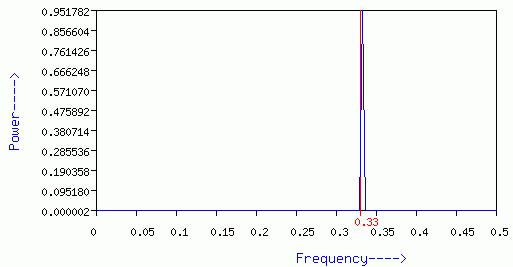
 Figure 1 :- Spectrum showing perfect 3-base periodicity.
This definitely is not the case with the coding sequences where the spectral
density because: a) has a much lower value at frequency 0.333 and b) shows
significant activity at all frequencies. Returning to the sequence A--A--A-
-A--..... , destroy the perfect repetition of base A by randomly replacing it
with G, C or T.
Figure 1 :- Spectrum showing perfect 3-base periodicity.
This definitely is not the case with the coding sequences where the spectral
density because: a) has a much lower value at frequency 0.333 and b) shows
significant activity at all frequencies. Returning to the sequence A--A--A-
-A--..... , destroy the perfect repetition of base A by randomly replacing it
with G, C or T.
 Figure 2 :- Spectrum with perfect repetition destroyed by replacing A with G, C ot T.
The spectral frequency value at frequency 0.33 has been reduced to a very sim-
-ilar to that observed in real coding sequences, while at the same time we
observe activity at all frequencies due to the random break-up of the perfect
repetition of base A.
Figure 2 :- Spectrum with perfect repetition destroyed by replacing A with G, C ot T.
The spectral frequency value at frequency 0.33 has been reduced to a very sim-
-ilar to that observed in real coding sequences, while at the same time we
observe activity at all frequencies due to the random break-up of the perfect
repetition of base A.
 Figure 3 :- Protein coding DNA sequence
These results indicate that certain periodicities are detectable in coding
sequences. This periodicity is not however perfect (as expected for real coding
sequences), but broken in many places and provide a mechanism in explaining the
global structure of coding sequences (Tsonis et al., 1991).
Figure 3 :- Protein coding DNA sequence
These results indicate that certain periodicities are detectable in coding
sequences. This periodicity is not however perfect (as expected for real coding
sequences), but broken in many places and provide a mechanism in explaining the
global structure of coding sequences (Tsonis et al., 1991).
 or
or
 The term 2pi appears because there are 2 radians per wavelength. Fourier
analysis of complex wave functions dissociates them into a Fourier series of
simple wave functions such as f(x). We could write a Fourier series containing
n terms as
The term 2pi appears because there are 2 radians per wavelength. Fourier
analysis of complex wave functions dissociates them into a Fourier series of
simple wave functions such as f(x). We could write a Fourier series containing
n terms as

 This shows that any complex wave can be expressed as a composite of simpler
cosine or sine waves.
If a complex discontinuous function is periodic (although this is not essen-
-tial ) with a period T such that f ( t + T ) = f ( t ), it may be represented
as a Fourier series of the form
This shows that any complex wave can be expressed as a composite of simpler
cosine or sine waves.
If a complex discontinuous function is periodic (although this is not essen-
-tial ) with a period T such that f ( t + T ) = f ( t ), it may be represented
as a Fourier series of the form
 where t is time, n is the number of components in the series, i is the imagi-
-nary number (= -1)1/2 and a, b, c etc. are coefficients describing the indi-
-vidual waves in the series.
This mathematically expresses the fact that a discontinuous function can be
dissected into individual sine/cosine wave functions which may in turn be
summed to arrive at an expression for it as a function ( in this case ) of time.
The relationship between the two sets of functions can be generalised with a
pair of equations which are Fourier transforms of each other.
where t is time, n is the number of components in the series, i is the imagi-
-nary number (= -1)1/2 and a, b, c etc. are coefficients describing the indi-
-vidual waves in the series.
This mathematically expresses the fact that a discontinuous function can be
dissected into individual sine/cosine wave functions which may in turn be
summed to arrive at an expression for it as a function ( in this case ) of time.
The relationship between the two sets of functions can be generalised with a
pair of equations which are Fourier transforms of each other.
 where i2 = -1.
A good practical analogy for Fourier analysis is the diffraction of white light
from the sun after passage through a prism into waves of individual frequency
and amplitude. The strength of sunlight incident on the prism may be expected to
vary with time which, in turn leads to variation in the amplitude of each
diffracted frequency. The prism therefore acts to transform a strength-time
domain into an amplitude-frequency domain.
The Fourier transform is special because the equation relating sets of numbers
which can be interconverted by the Fourier transform contains sine and cosine
terms allowing us to relate the complex wave to a series of simpler waves in a
fixed and meaningful way. This allows us to determine unknown discontinuous
experimental functions such as the electron density of an atom ( a function in
space ) or the electromagnetic spectrum of a molecule ( the time-inverse
function, frequency ).
The reason the Fourier transform is so widely used is that it offers specific
computational advantages over other mathematical approaches. However
complex the Fourier series, it is related to the original function by a
comparatively simple equation making it possible to move from the real-world
domain of space or time to the Fourier domain of frequency, phase and
amplitude. Moreover, considerable error can accumulate due to shortcomings in
real-world experimental systems such as those used in diffraction or spectroscopy.
Development of fast Fourier transform algorithm has facilitated very rapid
calculation by computer in the Fourier domain which can smooth out and
diminish this error resulting in a more accurate overall measurement. The
Fourier transform therefore provides a computationally versatile tool to analyse
complex functions arising from experimental measurements by dissecting them
into simpler wave functions which can be used to determine experimental
unknowns.
where i2 = -1.
A good practical analogy for Fourier analysis is the diffraction of white light
from the sun after passage through a prism into waves of individual frequency
and amplitude. The strength of sunlight incident on the prism may be expected to
vary with time which, in turn leads to variation in the amplitude of each
diffracted frequency. The prism therefore acts to transform a strength-time
domain into an amplitude-frequency domain.
The Fourier transform is special because the equation relating sets of numbers
which can be interconverted by the Fourier transform contains sine and cosine
terms allowing us to relate the complex wave to a series of simpler waves in a
fixed and meaningful way. This allows us to determine unknown discontinuous
experimental functions such as the electron density of an atom ( a function in
space ) or the electromagnetic spectrum of a molecule ( the time-inverse
function, frequency ).
The reason the Fourier transform is so widely used is that it offers specific
computational advantages over other mathematical approaches. However
complex the Fourier series, it is related to the original function by a
comparatively simple equation making it possible to move from the real-world
domain of space or time to the Fourier domain of frequency, phase and
amplitude. Moreover, considerable error can accumulate due to shortcomings in
real-world experimental systems such as those used in diffraction or spectroscopy.
Development of fast Fourier transform algorithm has facilitated very rapid
calculation by computer in the Fourier domain which can smooth out and
diminish this error resulting in a more accurate overall measurement. The
Fourier transform therefore provides a computationally versatile tool to analyse
complex functions arising from experimental measurements by dissecting them
into simpler wave functions which can be used to determine experimental
unknowns.
Figure 1 :- Spectrum showing perfect 3-base periodicity. This definitely is not the case with the coding sequences where the spectral density because: a) has a much lower value at frequency 0.333 and b) shows significant activity at all frequencies. Returning to the sequence A--A--A- -A--..... , destroy the perfect repetition of base A by randomly replacing it with G, C or T.
Figure 2 :- Spectrum with perfect repetition destroyed by replacing A with G, C ot T. The spectral frequency value at frequency 0.33 has been reduced to a very sim- -ilar to that observed in real coding sequences, while at the same time we observe activity at all frequencies due to the random break-up of the perfect repetition of base A.
Figure 3 :- Protein coding DNA sequence These results indicate that certain periodicities are detectable in coding sequences. This periodicity is not however perfect (as expected for real coding sequences), but broken in many places and provide a mechanism in explaining the global structure of coding sequences (Tsonis et al., 1991).