The predictive performance of any method can be calculated using threshold independent or threshold dependent parameters. Both parameters has their own advantages and drawbacks. Below are the descriptions and matematical equation used in calculating these parameters

In a binary prediction model (e.g. presence / absence) such as a 2-group discriminant analysis there are two possible prediction errors: false positives (FP) and false negatives (FN). The performance of a binary prediction model is normally summarized in a confusion or error matrix that cross-tabulates the observed and predicted + / - patterns.




	Actual +	Actual -
Predicted +	a	b
Predicted -	c	d




The left upper cell represents the number of peptides that have been correctly predicted as binders (TP), while the right lower cell represents the number of correctly predicted non-binders (TN). The other two cells are the number of peptides for which prediction and reality disagree. That is the number of binders predicted as non-binders (FN) and the number of non-binders predicted as binders (FP).
Several measures have been proposed to capture the information in a 2X2 table to a single scalar. The most widely used measures of are Sensitivity (Sn), Specificity (Sp), Positive Porbability Value (PPV) and Negative Probability Value (NPV).

These are defined as:

Sensitivity:
Also known as coverage of binders, the sensitivity is the percent of binders that are correctly predicted as binders. Higher sensitivity means that almost all of the potential binders will be included in the predicted results. However, at the same time some of the non-binders will also be predicted as binders. Therefore, the coverage is increased at the cost of PPV.

Specificity:
The specificity is the percent of correctly predicted as non-binders. It is similar to sensitivity. The sensitivity is for binders and specificity is for non-binders.

Positive Porbability Value (PPV):
It is the probability that a predicted binder will actually a binder. In other words, the PPV gives the confidence in predicted results. Higher probability means that there is very much chance that a predicted binder will actually be a binder. At the same time at higher PPV, we may loose some potential binders and the sensitivity or coverage may be less.

Negative Probability Value (NPV):
It is the probability that a predicted non-binder will actually be a non-binder. It is similar to senstivity but specific for non-binders.



Parameter	Brief description	Formulae
Sensitivity (Sn)	The proportion of correctly predicted binders	(a/(a + c))*100
Specificity (Sp)	The proportion of correctly predicted non-binders	(d/(b + d))*100
Positive Porbability Value (PPV)	The probability that a predicted binder will actually be a binder	(a/(a + b))*100
Negative Porbability Value (NPV)	The probability that a predicted non-binder will actually be a non-binder	(d/(c + d))*100


Note that all these parameters are conditional probabilities. For example if x denotes the actual state of a given peptide (b for binder and n for non-binder), and F(x) is the predicted state for such peptide, then Sn = P( F(x) = b|x = b) and Sp = P(x = b | F(x) = b). Therefore, we can have a high sensitivity with low specificity, for instance, every peptide predicted as binder or vice-versa. Therefore, neither of these parameters alone constitutes a good measure of global performance.

Accuracy:
The term accuracy was defined to provide a single measure of performance. It is defined as the proportion of correctly predicted peptides. The parameter provides a single valued approximation of the confusion matrix. The accuracy provided a good measure of performance. It is being used widely in evaluations of prediction methods. However, it shows some bias when the data set is unbalanced that is contains unequal number of binder and non-binders. The values of accuracy would be higher for thresholds favoring the correct prediction of binders (if number of binders are more than non-binders) or non-binders (in the number of non-binders are more than binders).

Dfactor:
The accuracy is calculated based on number of binders and non-binders therefore show bias on unbalanced set. The term Dfactor is the sum of percent sensitivity and specificity. Because the Dfactor takes percent rather than actual figures, it is relatively less affected by the unbalancing.

Correlation Coefficient (CC):
It is also known as Simple Matching Coefficient (SMC). The CC is more often in gene-prediction than in epitope prediction the correlation coefficient (CC) is used. Although CC, as defined above, has received different names, the formula described in table is the only special formulae for the Pearson product-moment correlation coefficient in the particular case of two binary variables. CC depends not only on sensitivity and specificity, but also on PPV and NPV. However, it has an undesirable property that it is not defined when either the prediction or the reality does not contain both binders and non-binders.

Parameter	Brief description	Formulae
Accuracy	The proportion of correctly predicted peptides (both binders and non-binders)	((a + d)/(a + b + c + d))*100
Dfactor	The sumation of sensitivity and specificity	((a/(a + c)) + (d/(b + d)))*100

Corelation Coefficient (CC)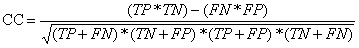



All of the measures described in this section depend on the values assigned to a, b, c & d in the confusion matrix. These values are obtained by the application of a threshold criterion to a continuous variable generated by the classifier. Typically, the classifier generates a variable that has values within the range 0 - 1 to which a 0.5 threshold is applied. Thus, a continuous, or at least ordinal, variable is dichotomized. If the threshold criterion is altered, the values in the confusion matrix will change. Often, the raw scores are available so it is relatively easy to examine the effect of changing the threshold. Even with techniques such as decision trees, which appear to use dichotomous variables, the software will have dichotomized a continuous variable.
There are number of reasons why the threshold value may need to be examined. For example, unequal group sizes (prevalence) can influence the scores for many of the classifier methods. This is particularly true for logistic regression, which produces scores biased towards the larger group (Hosmer & Lemeshow 1989). Similarly, if we have decided that FN errors are more serious than FP errors the threshold can be adjusted to decrease the FN rate at the expense of an increased FP error rate.
There is an alternative solution to threshold adjustments. This method makes use of all of the information contained within the original continuous variable and calculates threshold independent measures.

B. The Threshold independent parameters



One problem with the threshold dependent measures is their failure to use all of the information provided by a classifier. Although dichotomous classifications are convenient for decision making they can introduce distortions. The medical literature has recognized these problems and other measures have been introduced. In particular, the use of threshold-independent Receiver Operating Characteristic (ROC) Plots has received considerable attention. (ROC plots are now included in SPSS v9.0).
A ROC plot is obtained by plotting all sensitivity values (true positive fraction) on the y axis against their equivalent (1 - specificity) values (false positive fraction) for all available thresholds on the x axis, as in the example shown below.




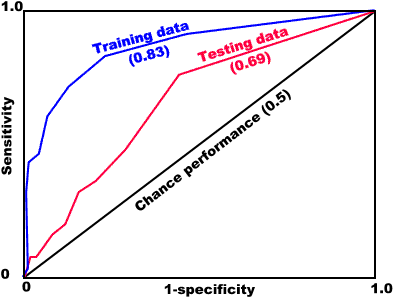
The area under the ROC function (AUC) is usually taken to be an important index because it provides a single measure of overall accuracy that is not dependent upon a particular threshold. The value of the AUC is between 0.5 and 1.0. If the value is 0.5 the scores for two groups do not differ, while a score of 1.0 indicates no overlap in the distributions of the group scores. Typically, values of the AUC will not achieve these limits. A value of 0.8 for the AUC means that for 80% of the time a random selection from the positive group will have a score greater than a random selection from the negative class.